Booth%27s Algorithm Calculator

by

This small project was an assignment for

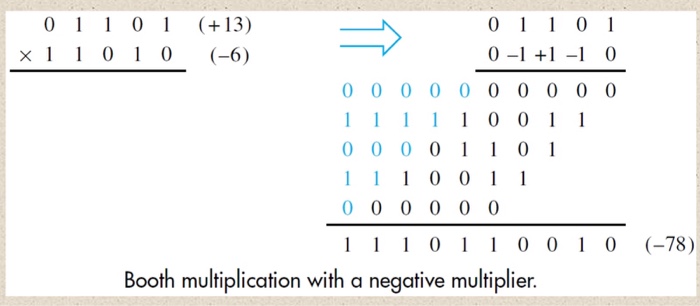
Booth's Algorithm. Fast Multiplication - Booth's Algorithm The Booth's algorithm serves two purposes: Fast multiplication (when there are consecutive 0's or 1's in the multiplier). Signed multiplication. First consider two decimal multiplications:. It is obvious that If straight forward multiplication is used, the first one is easier than the second as only. Calculator: Booth's Algorithm This small project was an assignment for CS 441 - Computer Architecture during Fall 2016 at UW Stout. I completed this project with Abby Peterson. Efficient Multiplication: Booth’s Algorithm Take advantage of circuits where shifting is cheaper than adding, or where space is at a premium. When multiplying by certain values (e.g. 99), it can be easier to think of this operation as a difference between two products.

CS 441 - Computer Architecture during Fall 2016 at UW Stout. I completed this project with Abby Peterson. We were allowed to use any programming language we wanted. Abby and I chose to use JavaScript and HTML/CSS because we wanted to get experience in a language we hadn't used in class.

Project Details


  1. Write program to calculate 8-bit Booth's Multiplier
  2. Input in decimal
  3. Output in both binary and decimal
  4. Show all steps
  5. Choose any programming language you're comfortable with

The Process


Writing the actual Booth's algorithm was quick and easy. The vast majority of the code was formatting. I had some HTML/CSS experience from middle school, but neither Abby nor I had ever used JavaScript. Luckily, it's pretty easy to learn. CSS was pretty frustrating. I had forgotten how finicky it can seem when you aren't fluent in it.
I planned on adding the ability to customize the number of bits (and I hate hard-coding data), so I made the number of bits a global variable and set it in cs441p1_submit(). This ended up being a life saver. I found out that the homework required a different number of bits than I had originally set. Rather than changing countless lines of code, I only changed the 'bit' variable.
We used the toString() and parseInt() functions a lot, because the made it super easy to translate from binary to decimal and vice versa.
BoothOne improvement we could have made was using HTML5 tags, especially for the form input options.
Here is the final result:
Algorithm
Booth%27s Algorithm CalculatorView on GitHub

© CalculatorSoup
Calculator

Calculator Use

Booth's Algorithm Calculator

Enter two whole numbers to find the greatest common factor (GCF). See the work and learn how to find the GCF using the Euclidean Algorithm.

How to Find the GCF Using Euclid's Algorithm

  1. Given two whole numbers where a is greater than b, do the division a ÷ b = c with remainder R.
  2. Replace a with b, replace b with R and repeat the division.
  3. Repeat step 2 until R=0.
  4. When R=0, the divisor, b, in the last equation is the greatest common factor, GCF.

Since greatest common factor (GCF) and greatest common divisor (GCD) are synonymous, the Euclidean Algorithm process also works to find the GCD.

Booth 27s Algorithm Calculator Online

Related Calculators

To find the GCF of more than two values see our Greatest Common Factor Calculator.

For more information and examples using the Euclidean Algorithm see our GCF Calculator and the section on Euclid's Algorithm.

References

The Math Forum: LCD, LCM.

Booth 27s Algorithm Calculator Download

Bureau 42: The Euclidean Algorithm: Greatest Common Factors Through Subtraction.

Booth 27s Algorithm Calculator Instructions

Rutgers University Department of Mathematics: The Euclidean Algorithm.

Cite this content, page or calculator as:

Booth 27s Algorithm Calculator Free

Furey, Edward 'Euclid's Algorithm Calculator'; CalculatorSoup, https://www.calculatorsoup.com - Online Calculators